what is nn?

前言

$$这篇blog的题目是What is NN? 很浮夸，是吧。一篇文章怎么能说清NN？(因为我也没打算说清楚，哈哈。)不过，NN是一个神奇的东西，它极具魅力，吸引着当下百分之九十的数据科学家和数据分析爱好者(包括我在内)。无论是写论文还是做项目，若不言NN，很容易被许多伪数据科学爱好者嗤之以鼻。因此，在现实的需求和洪流面前，我又不得不去看它。

$$从大二寒假开始，我就一直在看NN。无奈当时太年轻(当然现在依旧是，哈哈)，找到了邱锡鹏的《nndl-book》就开始大读特读。读了20多页，全是：

$$但现在，学了《机器学习》《回归分析》《多元统计分析》等专业课，被统计专业一群大佬老师熏陶了这么久。我感觉初窥了NN的门径，有必要写点什么记录一下近期的思考。题目很大，就叫《What is NN?》，哈哈。

NN

$$如果你问我，你觉得机器学习是什么？我可能会回答："机器学习就是函数逼近。"邱锡鹏在《nndl-book》这本书里阐述道："通俗地讲，机器学习（Machine Learning，ML）就是让计算机从数据中进行自动学习，得到某种知识（或规律）。"在我看来，这种知识或者规律，其最直观的体现就是我们通过数据训练出来的映射函数$$。

$$邱在《nndl-book》的第二章阐述了机器学习方法的三个基本要素：模型、学习准则、优化算法。NN作为一种现代的机器学习方法，自然也逃不开这个研究的基本范式。本文将主要关注NN的模型构造和理解，如若对后两者感兴趣请参阅邱锡鹏《神经网络与深度学习》。

定义

$$前馈神经网络(or多层感知机)是最早发明的人工神经网络，也是我们理解NN的基础。

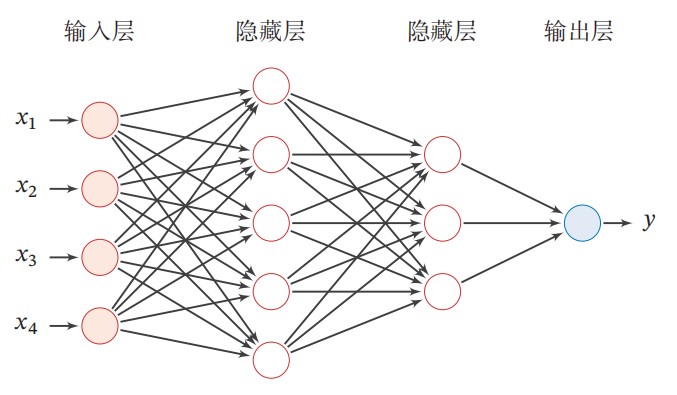
前馈神经网络

$$上图给出了一个前馈神经网络的示例。另外，我们再定义一些描述前馈神经网络的记号。

前馈神经网络的记号

记号	含义
$$	神经网络的层数
$$	第$$层神经元的个数
$$	第$$层神经元的激活函数
$$	第$$层到第$$层的权重矩阵
$$	第$$层到第$$层的偏置
$$	第$$层神经元的净输入(净活性值)
$$	第$$层神经元的输出(活性值)

$$令$$，前馈神经网络通过不断迭代下面公式进行信息传播：

$$

$$即首先根据第$$层Neuron的活性值(Activation,就是经过$$层的激活函数激活后的值)$$计算出第$$层Neuron的净活性值$$。然后经过一个激活函数(实则就是sigmoid/ReLu等非线性变换)得到第$$层神经元的活性值。

$$因此，我们也可以将每个神经层看作一个仿射变换(通过一个线性变换和平移/偏置)和一个非线性变换。

$$我们可以将上面的公式改写成：

$$

解读

Q1:NN示意图中圆圈的含义是？

$$我的理解是它们象征着净输入的各个分量或者说维度。一个圆圈代表该层输入的一个维度。

Q2:NN示意图中连线的含义是？

$$类比多因变量对多自变量的回归，单条连线指净输入某一维度/分量到下一层输入某一维度的变换。我们用$$表示某一层的净输入的话，再用$$分别表示该层变换输出(下一层输入)的第$$个维度、该层变换变换的权重矩阵第$$行、该层变换的偏置向量的第$$个分量，忽略非线性变换的步骤(毕竟只是一个外壳)，则单条连线象征的变换可表示为：

$$

$$在一本介绍PyTorch的书中，我看到了一些有趣的观点。

Q3:仿射变换

$$深度学习的核心组件之一是仿射变换，仿射变换是一个关于矩阵$$和向量$$的$$函数：

$$

$$在大部分书中，我们都能看到神经网络一层中的仿射变换变换被表示成了：

$$

$$实际上，可以写的“统计学”一些：

$$

$$这样做的好处就是可以更好理解为什么PyTorch在定义网络时，各层维度数字是首尾相连的。

Q4:非线性变换

$$首先，注意以下这个例子，它将解释为什么我们一层NN需要非线性函数。假设我们有两个仿射变换$$ 和$$。那么$$ 又是什么呢？

$$

$$是一个矩阵，$$是一个向量，可以看出，两个仿射变换的组合还是一个仿射变换。由此可以看出，使用以上方法将多个仿射变换组合成的长链式的神经网络，相对于单个仿射变换并没有性能上的提升。但是如果我们在两个仿射变换之间引入非线性，那么结果就大不一样了，我们可以构建出一个高性能的模型。

$$最常用的核心的非线性函数有：$$。你可能会想： “为什么是这些函数？明明有其他更多的非线性函数。”这些函数常用的原因是它们拥有可以容易计算的梯度，而计算梯度是学习的本质。例如:

$$

虽然$$是非线性的，但是当参数的绝对值增长时，它的梯度会很快消失。而小梯度意味着很难学习。因此大部分人默认选择$$或者$$。