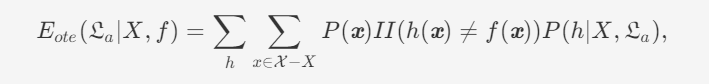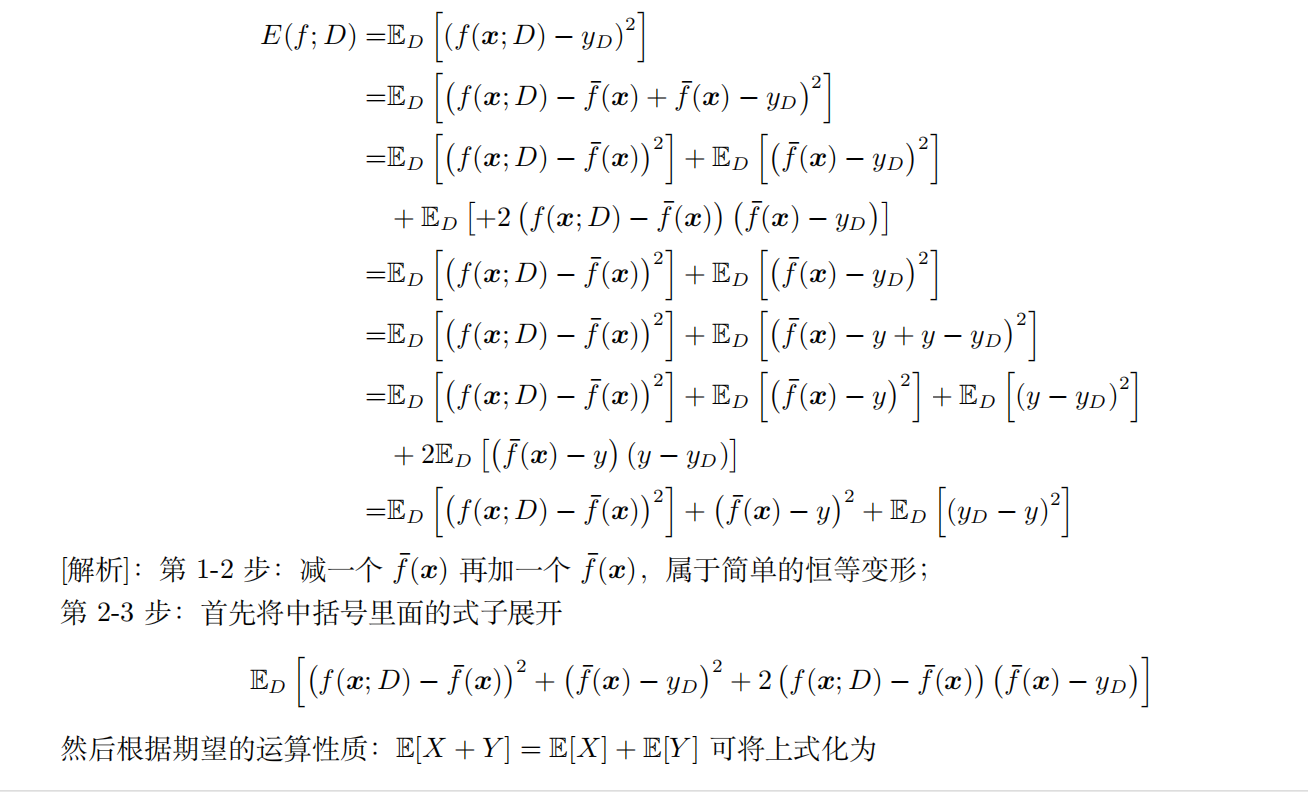ML-Lec1AndLec2

写在前面

不知不觉中，大三生活已经加载完了近3/4，让我在间歇性堕落中略感惶恐。有些无用的忙碌也让人厌恶。生活不易，且行且停，在大三的闲暇时刻，花点时间把之前学过的一些课程总结一下，或许也是一件美事。想来想去，先从自己最擅长(bushi)或者说还记得最多的课程开始，因此便有了这个机器学习课堂笔记。希望我能在1个月内更完。哈哈！

( •̀ ω •́ )y

关于课堂

zuel《机器学习》由统数学院蒋锋教授开设，使用教材为周志华《机器学习》。考虑到学生理解能力有限，他在48学时的课程里只教授了一些简单的概念性知识，课堂作业为使用相关算法的实验报告。时间紧，任务重，想拿到高分并不容易。

在学习这门课的过程中，我最大的收获是1个月入门R语言，熟悉使用Rmarkdown进行文本编辑写作。在折腾中知道了Latex、tidy verse、datatable等有趣的东西，自娱自乐，一度成为R吹。但是现在我还是主要使用Python，可能有点初恋情结(bushi)。在调用机器学习算法包进行实践时，R or Python都有其一套完善的workflow，二者精其一即可。当然都熟悉是最好的。

上课期间，印象最深的事情就是，有节课教室里都是水！当时大教室漏雨，整个地面都是水，我拿着西瓜书，踩着拖鞋，端着五食堂的绿茶，吧唧吧唧地趟着水喝着茶，从教室前走到教室后，然后慢悠悠地开始上课。感觉那节课是湿的，但是讲的都是干货，在那样的课堂上好有意思！

NFL定理

一二节课自古以来都比较水，《机器学习》自然不能免俗。除了交代了机器学习中一些比较重要的基础概念，重点1就是No Free Lunch Theorem(NFL，没有免费午餐定理)。

NFL定理最重要的寓意，就是让我们清楚地认识到，脱离具体问题或者数据，空泛地谈论“什么学习算法更好”毫无意义。因为若考虑所有潜在的问题，所有学习算法都一样好。

下面我们来简单证明一下(参见西瓜书P8)。

为简单起见，假设样本空间\(\mathcal{X}\)和假设空间\(\mathcal{H}\)都是离散的。令\(P(h|X,\mathfrak{L}_a)\)代表学习算法\(\mathfrak{L}_a\)基于训练数据\(X\)产生假设\(h\)的概率(这里的\(h\)说白了就是由数据拟合出来的，一个模拟真实目标函数的逼近函数)，再令\(f\)代表我们希望学习的真实目标函数。\(\mathfrak{L}_a)\)的“训练集外误差”，即\(\mathfrak{L}_a)\)在训练集之外的所有样本上的误差(out of train set error?)为

其中\(II(\cdot)\)是指示函数，若\(\cdot\)为真则取值1，否则取值0。

考虑二分类问题，且真实目标函数可以是任何函数\(\mathcal{X} \mapsto \{0,1\}\)，函数空间为\(\{0,1\}^{|\mathcal{X}|}\)。对所有可能的\(f\)按均匀分布对误差求和，有

上式显示出，总误差与学习算法无关(与\(II(\cdot)\)无关)。即对于任意两个学习算法\(\mathfrak{L}_a\)和\(\mathfrak{L}_b\)，我们都有

\[ \sum_{f} E_{ote}(\mathfrak{L}_a|X,f)= \sum_{f} E_{ote}(\mathfrak{L}_b|X,f) \]

也就是说，无论学习算法\(\mathfrak{L}_a\)多聪明、学习算法\(\mathfrak{L}_b\)多笨拙，它们的期望性能是相同的。

偏差方差分解定理

关于各种评价指标、ROC曲线啥的，个人觉得根据任务选择合适的评价指标即可。所以直接跳过，记录一下第二个重点——偏差方差分解定理。

公式推导好长！

偏差-方差分解试图对学习算法的期望泛化错误率进行拆解。我们知道，算法在不同训练集上学得的结果很可能不同，即便这些训练集是来自同一个分布。对测试样本\(x\)，令\(y_D\)为\(x\)在数据集中的标记，\(y\)为\(x\)的真实标记，\(f(x;D)\)为训练集\(D\)上学得的模型\(f\)在\(x\)上的预测输出。以回归任务为例，学习算法的期望预测为

\[ \bar{f}(x) = \mathbb{E}_D[f(x;D)], \qquad (2.37) \]

tips:数据产生时有可能出现噪声使得\(y_D \not = y\)，\(x\)应该是加粗的向量，打不出来，md

使用样本数相同的不同训练集产生的方差为

\[ var(x) = \mathbb{E}_D[(f(x;D)-\bar{f}(x))^2] \qquad (2.38) \]

噪声为

\[ \epsilon^2 = \mathbb{E}_D[(y_D-y)^2]. \qquad (2.39) \]

期望输出与真实标记的差别称为偏差(bias)，即

\[ bias^2(x)=(\bar{f}(x)-y)^2 \qquad (2.40) \]

为便于讨论，假定噪声期望为零，即有\(\mathbb{E}_D[y_D-y]=0\)。通过简单的多项式展开合并，可对算法的期望泛化误差进行分解：

于是乎，

\[ E(f;D) = bias^2(x)+var(x)+\epsilon^2 \qquad (2.42) \]

偏差(2.40)度量了学习算法的期望预测与真是结果的偏离程度，即刻画了学习算法本身的拟合能力；方差(2.38)度量了同样大小的训练集的变动所导致的学习性能的变化，即刻画了数据扰动所造成的影响；噪声(2.39)则表达了在当前任务上任何学习算法所能达到的期望泛化误差的下界，即刻画了学习问题本身的难度(数据是否垃圾、质量不高，即数据观测记录与真实有差距，不准确，这时候算法就会在垃圾上得到垃圾)

那么我们如何缓解偏差-方差窘境呢？一般的做法是采用AutomaticDriven的方法（剪枝、正则等等）。此外我们还可以增加样本数目（理论泛化误差的上界与样本数目有关，样本数目越多则泛化误差越小，当样本数目趋于无穷时，误差也将趋于0），以及选择合适的样本（不同的算法对于样本分布存在不同的偏好）缓解偏差-方差窘境（然而这种方法在现实问题中很难被采用）。